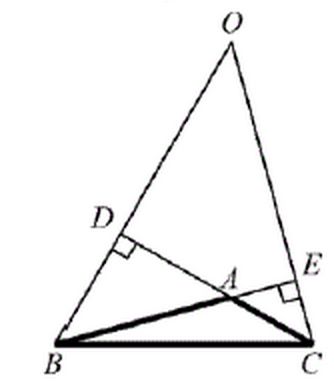
В треугольнике ABC угол A равен . Продолжения высот BD и CE, пересекаются в точке О. Найдите угол DOE. Ответ дайте в градусах.
Определение угла между высотами тупоугольного треугольника
Решение задачи
Данный урок показывает, как правильно использовать свойства углов треугольника, при нахождении градусной меры одного из углов. При решении задачи необходимо помнить о том, что прямоугольный треугольник (в данной задаче при проведении высот получается сразу несколько прямоугольных треугольников) – треугольник, у которого один из углов равен 90°. В этом случае однозначным является то, что сумма двух других углов также составляет 90°. По условию задачи известно значение тупого угла. Учитывая свойство вертикальных углов (углы, полученные при пересечении двух прямых) – вертикальные углы равны, и сумму углов четырехугольника: сумма углов четырехугольника равна 360° – можно выполнив элементарные арифметические действия получить значение искомого угла. Ответ получен.
Решение данной задачи рекомендовано для учащихся 7-х классов при изучении тем «Треугольники» («Треугольники»), «Соотношения между сторонами и углами треугольников» («Виды треугольников», «Задачи на углы треугольника», «Основные свойства прямоугольных треугольников»); для учащихся 8-х классов при изучении темы «Четырехугольники» («Многоугольники»). При подготовке к ЕГЭ урок рекомендован при повторении тем «Математический язык. Математическая модель», «Треугольники», «Соотношения между сторонами и углами треугольников», «Четырехугольники».
Отзывы учеников
-
 Светлана Иванова
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
 Влад Долгорукий
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
 Александр Шпик
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.