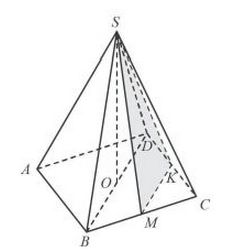
В правильной четырёхугольной пирамиде SABCD высота SO равна 13, диагональ основания BD равна 8. Точки K и M — середины ребер CD и BC соответственно. Найдите тангенс угла между плоскостью SMK и плоскостью основания ABC.
Нахождение тангенса угла между плоскостями в пирамиде
Решение задачи
Данный урок показывает решение геометрической задачи на нахождение значения тригонометрической функции — тангенса угла. Данное решение можно использовать с целью успешной подготовки к ЕГЭ по математике, в частности, при решении задач типа В13.
Условие задачи для наглядности изображается схематически на рисунке. Затем выполняется дополнительное построение: в плоскости из вершины пирамиды к прямой
опускается перпендикуляр. Также проводится диагональ
основания пирамиды. Согласно определению правильной четырехугольной пирамиды, ее основанием является квадрат. Следовательно, диагонали основания пирамиды пересекаются под прямым углом. Из этого делается вывод, что
— средняя линия в треугольнике
, при этом она перпендикулярна диагонали основания
. Для нахождения тангенса искомого угла
рассматривается треугольник
. Для этого используется следующее утверждение: тангенс острого угла в прямоугольном треугольнике — это отношение противолежащего катета к прилежащему. Таким образом,
, где
— высота пирамиды, а по свойству средней линии
. В итоге, выполнив действие деления, вычисляется искомая величина тангенса угла
.
Отзывы учеников
-
 Светлана Иванова
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
 Влад Долгорукий
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
 Александр Шпик
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.