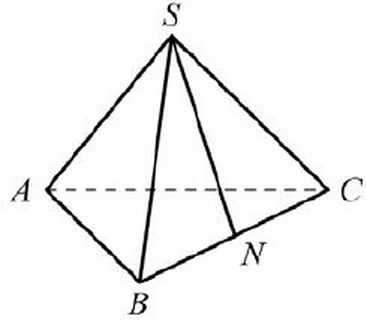
В правильной треугольной пирамиде SABC — N середина ребра BC, S — вершина. Известно, что SN=6, а площадь боковой поверхности равна 72. Найдите длину отрезка AB.
Нахождение стороны правильной треугольной пирамиды
Решение задачи
В данном уроке демонстрируется геометрическая задача, решение которой основывается на определении и свойствах правильной треугольной пирамиды. Утверждается, что все боковые грани правильной пирамиды являются равнобедренными треугольниками. Значит, площадь боковой поверхности данной пирамиды можно определить как бок. пов.=
. Далее в ходе решения рассматривается треугольник
, площадь которого равна половине произведения длины стороны на длину проведенной к этой стороне высоты. По свойству равнобедренного треугольника отрезок
— это одновременно медиана и высота, следовательно, верно следующее равенство:
. Выполнив соответствующую замену в формуле площади боковой поверхности пирамиды, подставляются известные по условию значения. Так как по определению правильной треугольной пирамиды в ее основании находится правильный треугольник, то найденное значение
равно искомой длине отрезка
.
Данная задача аналогична задачам вида В13, поэтому ее с успехом можно использовать в качестве подготовки к ЕГЭ по математике.
Отзывы учеников
-
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.