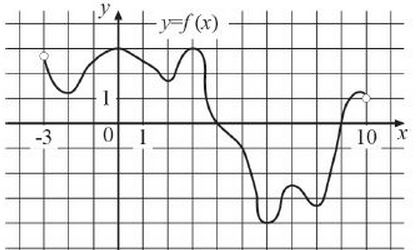
На рисунке изображён график функции , определённой на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
.
Нахождение точек экстремума функции
Решение задачи
В данном уроке рассматривается решение задачи, которое можно использовать в качестве примера при решении задач типа В9 при подготовке к ЕГЭ по математике.
Прежде всего, для решения задачи используется определение касательной — прямой, проходящей через точку кривой и совпадающей с ней в этой точке с точностью до первого порядка. Согласно условию, заданная прямая параллельна оси
. Соответственно, и касательные также должны быть параллельны данной оси. Утверждается, что касательные к графику функции параллельны оси
, если они проведены через точки экстремумов. Экстремум в математике — это максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Таким образом, решение задачи сводится к подсчету точек экстремумов (точек касания) на графике функции на интервале. При этом найденные точки нумеруются в порядке возрастания. Количество данных точек и является искомым ответом в задаче.
Отзывы учеников
-
 Светлана Иванова
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
 Влад Долгорукий
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
 Александр Шпик
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.