Диагонали параллелограмма пересекаются в точке
. В треугольнике
см, медиана
см. Найдите периметр параллелограмма
.
Нахождение периметра параллелограмма
Решение задачи
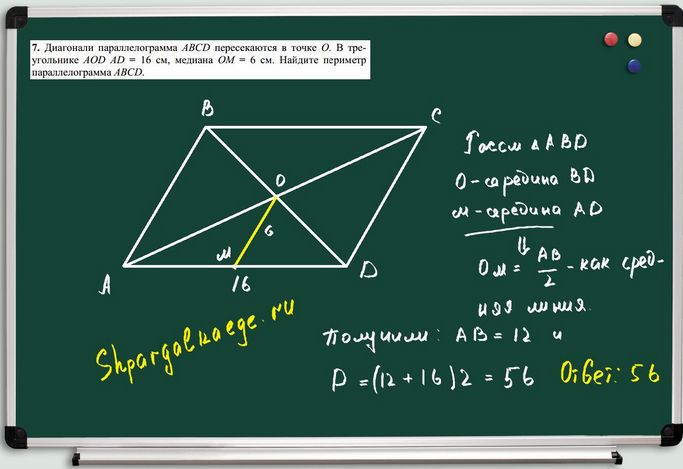
В данном уроке демонстрируется геометрическая задача, для успешного решения которой прежде всего следует изучить свойства параллелограмма и треугольника. Для наглядности условие задачи изображается схематически на рисунке. По свойству диагоналей параллелограмма точкой пересечения они делятся пополам, соответственно точка О — середина . А согласно определению медианы точка
— середина
. Таким образом, отрезок
— средняя линия треугольника
. По свойству средней линии треугольника, она параллельна третьей стороне и равна ее половине. Следовательно, верно равенство
. Зная длины сторон параллелограмма, искомый периметр определяется по формуле:
.
В случае использования данного решения в качестве примера для решения задач ОГЭ 9 подготовка к ОГЭ станет более успешной и результативной.
Отзывы учеников
-
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.