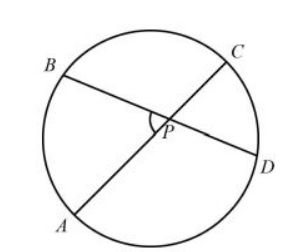
В окружности проведены хорды и
так, что они пересекаются в точке
(см. рис.). Докажите, что угол
равен полусумме угловых величин дуг
и
.
Геометрическая задача на доказательство
Решение задачи
В данном уроке демонстрируется пример решения геометрической задачи ОГЭ 13, которым целесообразно воспользоваться при подготовке к ОГЭ по математике.
Для решения на рисунке, заданном условием, производятся дополнительные построения: соединяются отрезками точки и
, а также
и
. Два вписанных угла треугольника
определяются с учетом правила: вписанный угол равен половине угловой величины дуги, на которую он опирается. А третий угол
выражается исходя из того, что сумма углов треугольника равна
. При этом учитывается тот факт, что сумма угловых величин всех дуг, из которых состоит заданная окружность, равняется
. Полученное таким образом выражение для определения угла
преобразовывается и упрощается. Окончательное выражение и доказывает утверждение, заданное условием и необходимое для ответа.
Отзывы учеников
-
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.