Тренировочный тест ЕГЭ по математике 11 класс
10.09.2014Тесты
В доме, в котором живет Женя, 9 этажей и несколько подъездов. На каждом этаже находится по 4 квартиры. Женя живет в квартире №45. В каком подъезде живет Женя?
Диагональ экрана телевизора равна 21 дюйму. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2.54 см. Результат округлите до целого числа сантиметров.
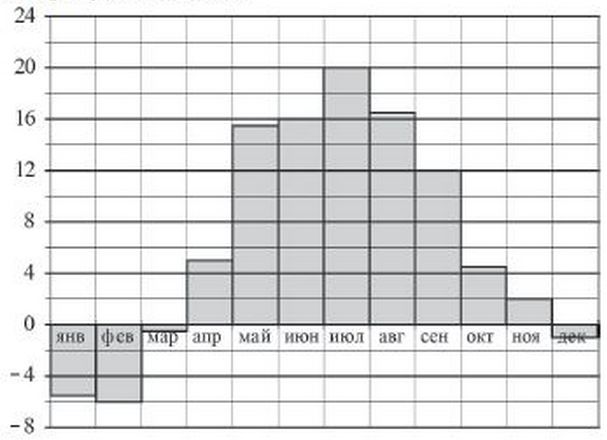
На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали - температура в градусах Цельсия. Какой из летних месяцев 2003 года в среднем был самым холодным? В ответе укажите среднюю температуру в этом месяце, в градусах Цельсия.
Автомобильный журнал определяет рейтинги автомобилей на основе показателей безопасности S, комфорта C, функциональности F, качества Q и дизайна D. Каждый отдельный показатель оценивается по -балльной шкале. Рейтинг R вычисляется по формуле
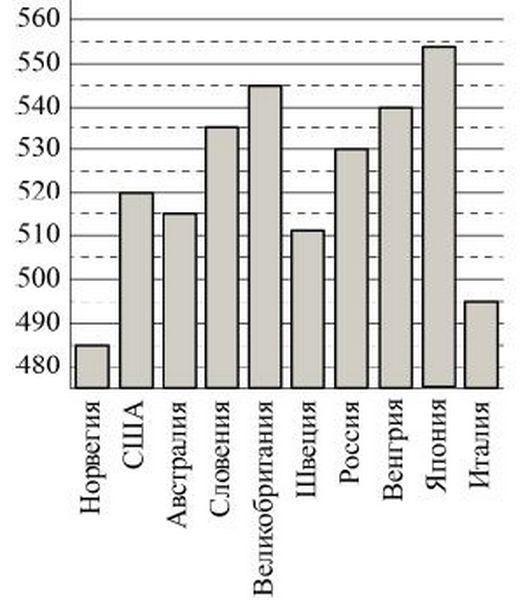
В таблице даны оценки каждого показателя для трёх моделей автомобилей. Определите наивысший рейтинг представленных в таблице моделей автомобилей.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 60% этих стекол, вторая - 40%. Среди стекол, выпускаемых первой фабрикой, брак составляет 3%. Среди стекол, выпускаемых второй фабрикой, брак составляет 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.
Если гроссмейстер А играет белыми, то он выигрывает у гроссмейстера Б с вероятностью 0.5. Если А играет черными, то А выигрывает у Б вероятностью 0.32. Гроссмейстеры А и Б играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А выиграет оба раза.
Найдите корень уравнения .
Найдите корень уравнения: .
Найдите , если
.
Расстояние от наблюдателя, находящегося на небольшой высоте километров над землёй, до наблюдаемой им линии горизонта вычисляется по формуле
, где
(км) - радиус Земли. С какой высоты горизонт виден на расстоянии
километров? Ответ выразите в километрах.
Мяч бросили под углом к плоской горизонтальной поверхности земли. Время полёта мяча ( в секундах) определяется по формуле
. При каком значении угла
(в градусах) время полёта будет равно
секунды, если мяч бросают с начальной скоростью
м/с ? Считайте, что ускорение свободного падения
м/
.
Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 15 км/ч, а вторую половину пути - со скоростью 90 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 54 км/ч. Ответ дайте в км/ч.
Первый сплав содержит 5% меди, второй - 14% меди. Масса второго сплава больше массы первого на 7 кг. Из этих двух сплавов получили третий сплав, содержащий 10% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.
Найдите наибольшее значение функции .
Найдите точку минимума функции .
а) Решите уравнение .
б) Найдите все корни этого уравнения, принадлежащие промежутку .
Правильные треугольники и
лежат в перпендикулярных плоскостях,
. Точка
- середина
, а точка
делит отрезок
так, что
. Вычислите объём пирамиды
.
Решите систему неравенств:
Боковые стороны KL И MN трапеции KLMN равны 7 и 25 соответственно. Отрезок, соединяющий середины диагоналей, равен 12, средняя линия трапеции равна 60. Прямые KL и MN пересекаются в точке A. Найдите радиус окружности, вписанной в треугольник ALM.
Отзывы учеников
-
 Светлана Иванова
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
 Влад Долгорукий
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
 Александр Шпик
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.