Математика B9
Тематикой раздела сайта Шпаргалка ЕГЭ, посвященного тому, как решать задачи ЕГЭ по математике B9, являются производные функции. Удобный интерфейс и логическое распределение каждого задания из вариантов ЕГЭ 2011 – 2019 годов способствуют быстрому и эффективному овладению этим сложным материалом.
В данном разделе изучаются и анализируются графики функций и производные функций, для чего используются прикладные задачи, имеющие непосредственное отношение к окружающей нас жизни. Такая методика исследование функций не только помогает заинтересовать и стимулировать учащихся. Она позволяет уже с подросткового возраста начать приспосабливать детей к будущей взрослой жизни.
Также следует отметить, что задания B9 ЕГЭ по математике обеспечивают максимально качественную подготовку учащихся к ответственным экзаменам. Здесь даются самые глубокие знания, представленные в доступном для понимания каждого формате. Поэтому Шпаргалка ЕГЭ пользуется невероятной популярностью, как среди учеников, так и у их родителей, проявляющих настоящую заботу о будущем своих детей.
Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки М со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s в метрах. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
Материальная точка M начинает движение из точки A и движется по прямой на протяжении 11 секунд. График показывает, как менялось расстояние от точки A до точки М со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s в метрах. Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
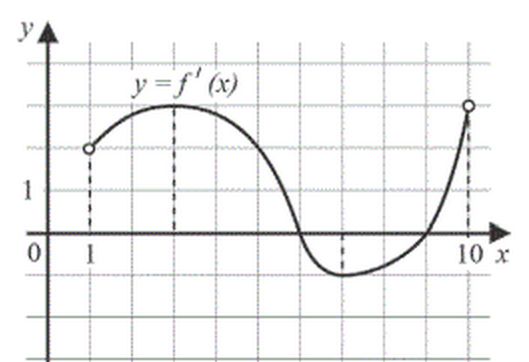
На рисунке изображён график производной функции
, определённой на интервале
. Найдите количество точек минимума функции
, принадлежащих отрезку
.
На рисунке изображён график производной функции
, определённой на интервале
. В какой точке отрезка
функция
принимает наименьшее значение?
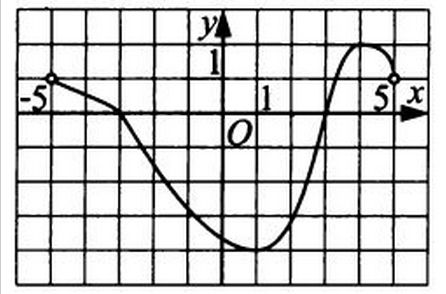
На рисунке изображён график функции — производной функции
, определённой на интервале
. Найдите точку минимума функции
.
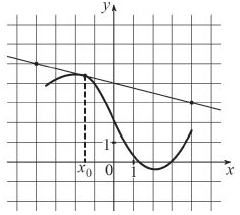
На рисунке изображены график функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
На рисунке изображены график дифференцируемой функции и касательная к нему в точке с абсциссой
. Найдите значение производной функции
в точке
.
На рисунке изображён график функции — производной функции
, определённой на интервале
. Найдите точку максимума функции
.
Функция определена и непрерывна на отрезке
. На рисунке изображён график её производной. Найдите точку
, в которой функция принимает наименьшее значение, если
больше либо равна
.
Отзывы учеников
-
 Светлана Иванова
Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
-
 Влад Долгорукий
Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С. Всем рекомендую Генератор Вариантов.
-
 Александр Шпик
Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.