Досрочный вариант ЕГЭ по математике

Установка двух счётчиков воды (холодной и горячей) стоит 2500 руб. До установки счётчиков Александр платил за воду (холодную и горючую) ежемесячно 1700 руб. После установки счётчиков оказалось, что в среднем за месяц он расходует воды на 1000 руб. при тех же тарифах на воду. За какое наименьшее количество месяцев при тех же тарифах на воду установка счётчиков окупится?

Магазин делает пенсионерам скидку на определенное количество процентов от цены покупки. Пакет кефира стоит в магазине 40 рублей. Пенсионер заплатил за пакет кефира 38 рублей. Сколько процентов составляет скидка для пенсионеров?   

На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса по математике в 2007 году (по 1000-балльной шкале). Найдите число стран, в которых средний балл ниже, чем 515. 

Строительной фирме нужно приобрести 40 кубометров строительного бруса у одного из трех поставщиков. Какова наименьшая стоимость покупки с доставкой (в рублях)? Цены и условия доставки приведены в таблице.

На клетчатой бумаге с размером клетки 1 см x 1 см изображён треугольник ABC. Найдите длину его высоты, опущенной на сторону AB.

В сборнике билетов по истории всего 50 билетов, в 13 из них встречается вопрос о Великой Отечественной войне. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос о Великой Отечественной войне.

Найдите корень уравнения:  .

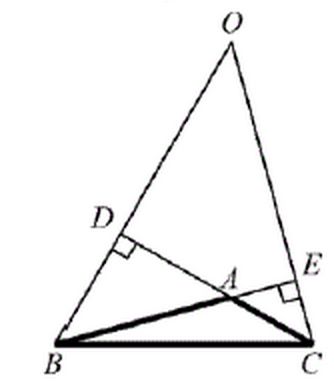
В треугольнике ABC угол A равен . Продолжения высот BD и CE, пересекаются в точке О. Найдите угол DOE. Ответ дайте в градусах.

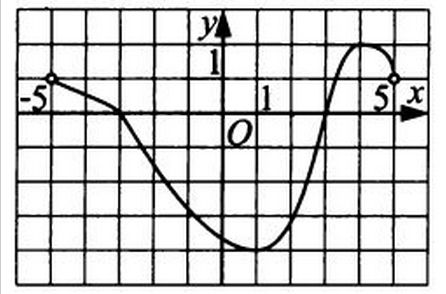
Функция   определена и непрерывна на отрезке . На рисунке изображён график её производной. Найдите точку , в которой функция принимает наименьшее значение, если  больше либо равна .

Шар, объём которого равен , вписан в куб. Найдите объём куба.

Найти значения выражения:  .

Автомобиль, движущийся в начальный момент со скоростью  м/с, начал торможение с постоянным ускорением  м/. За t секунд после начала торможения он прошёл путь   (м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал  метров. Ответ выразите в секундах.   

В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рис.). Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху?

Дорога между пунктами A и B состоит из подъёма и спуска, а ее длина равна 8 км. Пешеход прошёл путь из A в B за 2 часа 45 минут. Время его движения на спуске составило 1 час 15 минут. С какой скоростью пешеход шёл на спуске, если скорость его движения на подъёме меньше скорости движения на спуске на 2 км/ч? Ответ выразите в км/ч.

Найдите точку максимума функции:  . 

а) Решите уравнение: .

б) Укажите корни этого уравнения, принадлежащие отрезку . 

Радиус основания конуса с вершиной  равен 6, а длина его образующей равна 9. На окружности основания конуса выбраны точки  и , делящие окружность на две дуги, длины которых относятся как 1:3. Найдите площадь сечения конуса плоскостью .  

Решите систему неравенств: 

Около остроугольного треугольника  описана окружность с центром . На продолжении отрезка  за точку  отмечена точка  так, что .

а) Докажите, что четырёхугольник  - вписанный.

б) Найдите радиус окружности, описанной около четырёхугольника , если , а .

Найдите все значения , при которых уравнение имеет единственное решение.

.

На окружности некоторым образом расставили натуральные числа от 1 до 21 (каждое число поставлено по одному разу). Затем для каждой пары соседних чисел нашли разность большего и меньшего.

а) Могли ли все полученные разности быть не меньше 11?

б) Могли ли все полученные разности быть не меньше 10?

в) Помимо полученных разностей, для каждой пары чисел, стоящих через одно, нашли разность большего и меньшего. Для какого наибольшего целого числа k можно так расставить числа, чтобы все разности были не меньше k ?